Tabel t – apa itu tabel t? Pernahkan teman-teman mendengar tentang tabel z? Barangkali ada yang hanya sekali pernah mendengar tetapi hanya lewat, ada juga yang baru pertama ini mengetahui ada istilah tabel z.
Hal itu wajar saja, karena memang bagi banyak orang istilah ini masih terdengar asing.
Bahkan bagi pelajar SMP atau SMA dan bahkan mahasiswa tidak selalu memahami istilah tabel z ini.
Kalian akan merasa familiar dengan istilah tersebut jika mempalajari tentang statistik. Ya materi ini memang biasanya dipalajari dalam ilmu statistik.
Dan tidak semua orang mempelajari ilmu tersebut, meskipun mahasiswa yang notabene mendapatkan mata kuliah statistik belum tentu mengetahui benar apa yang dimaksud dengan tabel t.
Orang yang biasanya paham benar dengan istilah, atau juga penggunaan tabel tersebut pastilah sering bersinggungan dengan statistik.
Nah sayangnya seperti yang telah dijelaskan di atas materi statistik ini akan dipelajari ketika kamu masuk ke perguruan tinggi, karenanya suka atau tidak teman-teman harus mempelajarinya.
Meskipun tentu saja akan berhubungan dengan hitung menghitung tabel ini sebenarnya cukup membantu banyak.
Untuk mengetahui apa sebenarnya dan bagaimana penggunaan tabel tersebut yuk langsung saja simak uraiannya di bawah ini:
Pengertian Tabel t
Dalam statistik teman-teman akan menjumpai istilah distribusi normal. Nah jika sebelumnya kami telah membahas tentang tabel Z, nah tabel t ini kurang lebih sama dengan tabel Z.
Tabel t ini bermula dari dikembangkannya uji t oleh William Sealy Gosset.
Ia berpendapat kalau tabel Z kurang cocok cocok untuk sampel kecil. Sehingga kemudian dirinya mengembangkan tabel t , sebuah distribusi lain yang kurang lebih sama dengan distribusi normal.
Distribusi ini bisa digunakan untuk sampel yang berjumlah besar dan juga sampel kecil. Lalu sebenarnya untuk apa tabel ini?
Bisa dibilang tabel t berfungsi untuk membantu teman-teman menentukan hipotesis. Bagaimana caranya?
Yaitu dengan melakukan perbandingan antara statistik hitung dengan statistik uji.
Statistik hitung dilakukan dengan perhitungan sendiri secara manual, sedangkan statistik uji ini membutuhkan tabel distribusi.
Tabel distribusi ini disesuaikan dengan jenis uji yang dilakukan, misal jika statistik uji Z maka tabel distribusinya juga menggunakan tabel z.
Begitu pula jika yang dilakukan adalah statistik uji t, maka perbandingannya menggunakan tabel t. Adapun tabel distribusi t akan kami cantumkan pada pembahasan selanjutnya.
Tabel t
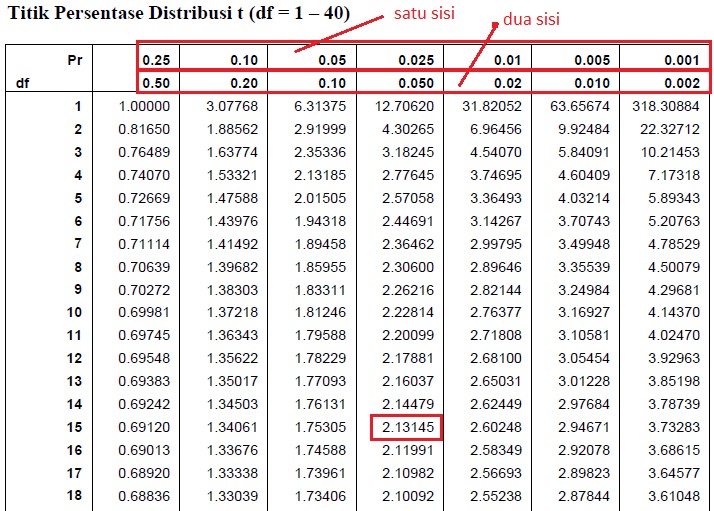
Berikut ini kami sajikan tabel t, untuk memudahkan teman-teman menggunakan statistik uji t:
| D.F. | TINGKAT SIGNIFIKANSI | ||||||
|---|---|---|---|---|---|---|---|
| Dua sisi | 20% | 10% | 5% | 2% | 1% | 0,2% | 0,1% |
| Satu sisi | 10% | 5% | 2,5% | 1% | 0,5% | 0,1% | 0,05% |
| 1 | 3, 078 | 6,314 | 12,706 | 31,821 | 63,657 | 318,309 | 636,619 |
| 2 | 1,886 | 2,920 | 4,303 | 6,965 | 9,925 | 22,327 | 31,599 |
| 3 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | 10,215 | b12,924 |
| 4 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | 7,173 | 8,610 |
| 5 | 1,476 | 2,015 | 2,571 | 3,365 | 4,032 | 5,893 | 6,869 |
| 6 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | 5,208 | 5,959 |
| 7 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | 4,785 | 5,408 |
| 8 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | 4,501 | 5,041 |
| 9 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | 4,297 | 4,781 |
| 10 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | 4,144 | 4,587 |
| 11 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | 4,025 | 4,437 |
| 12 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | 3,930 | 4,318 |
| 13 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | 3,852 | 4,221 |
| 14 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | 3,787 | 4,140 |
| 15 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 | 3,733 | 4,073 |
| 16 | 1,337 | 1,746 | 2,120 | 2,583 | 2,921 | 3,686 | 4,015 |
| 17 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 | 3,646 | 3,965 |
| 18 | 1,330 | 1,734 | 2,101 | 2,552 | 2,878 | 3,610 | 3,922 |
| 19 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | 3,579 | 3,883 |
| 20 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 | 3,552 | 3,850 |
| 21 | 1,323 | 1,721 | 2,080 | 2,518 | 2,831 | 3,527 | 3,819 |
| 22 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 | 3,505 | 3,792 |
| 23 | 1,319 | 1,714 | 2,069 | 2,500 | 2,807 | 3,485 | 3,768 |
| 24 | 1,318 | 1,711 | 2,064 | 2,492 | 2,797 | 3,467 | 3,745 |
| 25 | 1,316 | 1,708 | 2,060 | 2,485 | 2,787 | 3,450 | 3,725 |
| 26 | 1,315 | 1,706 | 2,056 | 2,479 | 2,779 | 3,435 | 3,707 |
| 27 | 1,314 | 1,703 | 2,052 | 2,473 | 2,771 | 3,421 | 3,690 |
| 28 | 1,313 | 1,701 | 2,048 | 2,467 | 2,763 | 3,408 | 3,674 |
| 29 | 1,311 | 1,699 | 2,045 | 2,462 | 2,756 | 3,396 | 3,659 |
| 30 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 | 3,385 | 3,646 |
| 31 | 1,309 | 1,696 | 2,040 | 2,453 | 2,744 | 3,375 | 3,633 |
| 32 | 1,309 | 1,694 | 2,037 | 2,449 | 2,738 | 3,365 | 3,622 |
| 33 | 1,308 | 1,692 | 2,035 | 2,445 | 2,733 | 3,356 | 3,611 |
| 34 | 1,307 | 1,691 | 2,032 | 2,441 | 2,728 | 3,348 | 3,601 |
| 35 | 1,306 | 1,690 | 2,030 | 2,438 | 2,724 | 3,340 | 3,591 |
| 36 | 1,306 | 1,688 | 2,028 | 2,434 | 2,719 | 3,333 | 3,582 |
| 37 | 1,305 | 1,687 | 2,026 | 2,431 | 2,715 | 3,326 | 3,574 |
| 38 | 1,304 | 1,686 | 2,024 | 2,429 | 2,712 | 3,319 | 3,566 |
| 39 | 1,304 | 1,685 | 2,023 | 2,426 | 2,708 | 3,313 | 3,558 |
| 40 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 | 3,307 | 3,551 |
| 41 | 1,303 | 1,683 | 2,020 | 2,421 | 2,701 | 3,301 | 3,544 |
| 42 | 1,302 | 1,682 | 2,018 | 2,418 | 2,698 | 3,296 | 3,538 |
| 43 | 1,302 | 1,681 | 2,017 | 2,416 | 2,695 | 3,291 | 3,532 |
| 44 | 1,301 | 1,680 | 2,015 | 2,414 | 2,692 | 3,286 | 3,526 |
| 45 | 1,301 | 1,679 | 2,014 | 2,412 | 2,690 | 3,281 | 3,520 |
| 46 | 1,300 | 1,679 | 2,013 | 2,410 | 2,687 | 3,277 | 3,515 |
| 47 | 1,300 | 1,678 | 2,012 | 2,408 | 2,685 | 3,273 | 3,510 |
| 48 | 1,299 | 1,677 | 2,011 | 2,407 | 2,682 | 3,269 | 3,505 |
| 49 | 1,299 | 1,677 | 2,010 | 2,405 | 2,680 | 3,265 | 3,500 |
| 50 | 1,299 | 1,676 | 2,009 | 2,403 | 2,678 | 3,261 | 3,496 |
| 51 | 1,298 | 1,675 | 2,008 | 2,402 | 2,676 | 3,258 | 3,492 |
| 52 | 1,298 | 1,675 | 2,007 | 2,400 | 2,674 | 3,255 | 3,488 |
| 53 | 1,298 | 1,674 | 2,006 | 2,399 | 2,672 | 3,251 | 3,484 |
| 54 | 1,297 | 1,674 | 2,005 | 2,397 | 2,670 | 3,248 | 3,480 |
| 55 | 1,297 | 1,673 | 2,004 | 2,396 | 2,668 | 3,245 | 3,476 |
| 56 | 1,297 | 1,673 | 2,003 | 2,395 | 2,667 | 3,242 | 3,473 |
| 57 | 1,297 | 1,672 | 2,002 | 2,394 | 2,665 | 3,239 | 3,470 |
| 58 | 1,296 | 1,672 | 2,002 | 2,392 | 2,663 | 3,237 | 3,466 |
| 59 | 1,296 | 1,671 | 2,001 | 2,391 | 2,662 | 3,234 | 3,463 |
| 60 | 1,296 | 1,671 | 2,000 | 2,390 | 2,660 | 3,232 | 3,460 |
| 61 | 1,296 | 1,670 | 2,000 | 2,389 | 2,659 | 3,229 | 3,457 |
| 62 | 1,295 | 1,670 | 1,999 | 2,388 | 2,657 | 3,227 | 3,454 |
| 63 | 1,295 | 1,669 | 1,998 | 2,387 | 2,656 | 3,225 | 3,452 |
| 64 | 1,295 | 1,669 | 1,998 | 2,386 | 2,655 | 3,223 | 3,449 |
| 65 | 1,295 | 1,669 | 1,997 | 2,385 | 2,654 | 3,220 | 3,447 |
| 66 | 1,295 | 1,668 | 1,997 | 2,384 | 2,652 | 3,218 | 3,444 |
| 67 | 1,294 | 1,668 | 1,996 | 2,383 | 2,651 | 3,216 | 3,442 |
| 68 | 1,294 | 1,668 | 1,995 | 2,382 | 2,650 | 3,214 | 3,439 |
| 69 | 1,294 | 1,667 | 1,995 | 2,382 | 2,649 | 3,213 | 3,437 |
| 70 | 1,294 | 1,667 | 1,994 | 2,381 | 2,648 | 3,211 | 3,435 |
| 71 | 1,294 | 1,667 | 1,994 | 2,380 | 2,647 | 3,209 | 3,433 |
| 72 | 1,293 | 1,666 | 1,993 | 2,379 | 2,646 | 3,207 | 3,431 |
| 73 | 1,293 | 1,666 | 1,993 | 2,379 | 2,645 | 3,206 | 3,429 |
| 74 | 1,293 | 1,666 | 1,993 | 2,378 | 2,644 | 3,204 | 3,427 |
| 75 | 1,293 | 1,665 | 1,992 | 2,377 | 2,643 | 3,202 | 3,425 |
| 76 | 1,293 | 1,665 | 1,992 | 2,376 | 2,642 | 3,201 | 3,423 |
| 77 | 1,293 | 1,665 | 1,991 | 2,376 | 2,641 | 3,199 | 3,421 |
| 78 | 1,292 | 1,665 | 1,991 | 2,375 | 2,640 | 3,198 | 3,420 |
| 79 | 1,292 | 1,664 | 1,990 | 2,374 | 2,640 | 3,197 | 3,418 |
| 80 | 1,292 | 1,664 | 1,990 | 2,374 | 2,639 | 3,195 | 3,416 |
| 81 | 1,292 | 1,664 | 1,990 | 2,373 | 2,638 | 3,194 | 3,415 |
| 82 | 1,292 | 1,664 | 1,989 | 2,373 | 2,637 | 3,193 | 3,413 |
| 83 | 1,292 | 1,663 | 1,989 | 2,372 | 2,636 | 3,191 | 3,412 |
| 84 | 1,292 | 1,663 | 1,989 | 2,372 | 2,636 | 3,190 | 3,410 |
| 85 | 1,292 | 1,663 | 1,988 | 2,371 | 2,635 | 3,189 | 3,409 |
| 86 | 1,291 | 1,663 | 1,988 | 2,370 | 2,634 | 3,188 | 3,407 |
| 87 | 1,291 | 1,663 | 1,988 | 2,370 | 2,634 | 3,187 | 3,406 |
| 88 | 1,291 | 1,662 | 1,987 | 2,369 | 2,633 | 3,185 | 3,405 |
| 89 | 1,291 | 1,662 | 1,987 | 2,369 | 2,632 | 3,184 | 3,403 |
| 90 | 1,291 | 1,662 | 1,987 | 2,368 | 2,632 | 3,183 | 3,402 |
| 91 | 1,291 | 1,662 | 1,986 | 2,368 | 2,631 | 3,182 | 3,401 |
| 92 | 1,291 | 1,662 | 1,986 | 2,368 | 2,630 | 3,181 | 3,399 |
| 93 | 1,291 | 1,661 | 1,986 | 2,367 | 2,630 | 3,180 | 3,398 |
| 94 | 1,291 | 1,661 | 1,986 | 2,367 | 2,629 | 3,179 | 3,397 |
| 95 | 1,291 | 1,661 | 1,985 | 2,366 | 2,629 | 3,178 | 3,396 |
| 96 | 1,290 | 1,661 | 1,985 | 2,366 | 2,628 | 3,177 | 3,395 |
| 97 | 1,290 | 1,661 | 1,985 | 2,365 | 2,627 | 3,176 | 3,394 |
| 98 | 1,290 | 1,661 | 1,984 | 2,365 | 2,627 | 3,175 | 3,393 |
| 99 | 1,290 | 1,660 | 1,984 | 2,365 | 2,626 | 3,175 | 3,392 |
| 100 | 1,290 | 1,660 | 1,984 | 2,364 | 2,626 | 3,174 | 3,390 |
Dari tabel di atas teman-teman akan melihat pembagian kolom atau nilai alpha. Alpha tersebut merupakan simbol dari probabilita atau taraf signifikansi.
Semakin kecil nilai alpha menunjukkan adanya probabilita satu arah, sebaliknya semakin besar nilai alpha menunjukkan adanya probabilita dua arah.
Misalnya pada nilai alpha 0,25 merupakan probabilita satu arah, sedangkan pada kolom 0,50 adalah probabilita dua arah.
Bagaimana Mencari Nilai T Tabel?
Pertama –tama kita harus tahu terlebih dahulu apa itu probabilita satu arah dan dua arah.
Ya probabilita satu arah digunakan jika hipotesis yang akan diuji juga merupakan hipotesis satu arah.
Contohnya “kemiskinan berpengaruh positif terhadap angka putus sekolah”.
Artinya jika semakin besar kemiskinan semakin banyak juga angka putus sekolah.
Di sini jelas hipotesis tersebut satu arah, yakni kemiskinan berpengaruh pada angka putus sekolah, tapi belum tentu sebaliknya.
Lalu bandingkan dengan hipotesis dua arah? Contohnya “terdapat pengaruh antara tingkat pendidikan dan pendapatan”.
Di sini terdapat hipotesis dua arah yakni adanya pengaruh antara pendidikan dan pendapatan, keduanya saling mempengaruhi.
Nah setelah kita tahu jenis hipotesis yang akan diuji, sekarang teman-teman harus menentukan derajat bebas atau df (degrre of freedom).
Caranya? Jika hipotesis bermodel regresi maka gunakan rumus :
n – k
ket:
n = banyaknya observasi
k = jumlah variabel
tetapi jika bukan model regresi rumusnya tentu akan berbeda-beda.
Contoh Kasus
Misalkan: Terdapat sebuah persamaan regresi yang memperlihatkan pengaruh pendidikan (X1) dan umur (X2) terhadap suatu pendapatan (Y).
Jumlah observasi (responden) yang digunakan untuk membentuk persamaan ini yaitu sebanyak 12 responden (jumlah sampel yang sedikit ini hanya untuk penyederhanaannya saja).
Pengujian hipotesis dengan α = 5%. Sedangkan derajat bebas pengujian adalah n – k = 12 – 3 = 9.
Hipotesis pertama: Pendidikan berpengaruh positif terhadap sebuah pendapatan. Pengujian dengan α = 5 %.
Hipotesis kedua: Umur berpengaruh terhadap sebuah pendapatan. Pengujian juga dengan menggunakan α = 5 %.
Untuk hipotesis pertama, karena uji satu arah, maka kita lihat pada kolom ke empat tabel diatas, sedangkan df nya kita lihat pada angka sembilan.
Nilai tabel t = 1,833. Untuk hipotesis kedua, karena uji dua arah, maka kita lihat pada kolom ke lima tabel diatas, dengan df = 9 maka nilai tabel t = 2,821
Bagaimana penjelasan di atas? apakah cukup menjawab pertanyaanmu tentang tabel t? Atau malah tambah bingung sebenarnya gimana sih menghitung tabel tersebut?
Kalau ada yang masih bingung tenang saja karena belajar materi ini memang cukup menguras kesabaran dan kekonsistenan.
Tetapi jikalau kebingungan itu timbulnya dari penjelasan kami yang rumit, tentu kami memohon maaf dan akan terus belajar lagi.
Cukup sekian artikel yang bisa kami sajikan, semoga bermanfaat meskipun dalam tingkat yang kecil. Sehat selalu teman-teman, selamat belajar!
Originally posted 2021-01-17 00:15:01.