Rumus trapesium – Halo kawan-kawan semua? Bagaimana kebarnya? Semoga sehat selalu ya. Kami kembali lagi untuk membagikan postingan-postingan seputar ilmu pengetahuan.
Kali ini kami akan membagikan tentang materi pelajaran matematika yang biasanya dikenalkan sejak sekolah dasar.
Apa itu? sesuatu yang berhubungan dengan bangun datar, tepatnya adalah tentang bangun datar bernama trapesium.
Bangun dua dimensi ini tidak hanya dipelajari ketika berada di bangku sekolah dasar saja, tetapi juga SMP dan SMA.
Meskipun kemudian semakin tinggi jenjang pendidikannya kesulitan dan kerumitan yang dipalajari tentang trapesium tentu berbeda.
Kalau di SD mungkin kita hanya akan menemukan soal yang mempertanyakan luas atau keliling trapesium dengan bentuk sederhana.
Sedangkan di tingkat lanjut biasanya bangun yang dipertanyakan tidak hanya trapesium saja tetapi digabungkan dengan beberapa bangun lainnya, sehingga terkadang akan sulit untuk mengidentifikasi bahwa gambar tersebut memuat bangun trapesium.
Karenanya kita harus mempelajarinya terus menerus, paling tidak supaya kita bisa menjawab soal tentang trapesium sesulit apapun itu.
Dan di bawah ini kami sudah menyiapkan beberapa pembahasan yang harus diketahui oleh teman-teman yang ingin belajar tentang trapesium, termasuk juga rumus trapesium.
Kalau begitu tanpa berlama-lama lagi, yuk langsung saja kita simak penjelasan berikut ini, barangkali bisa membantu teman-teman yang mebutuhkan.
Pengertian Trapesium
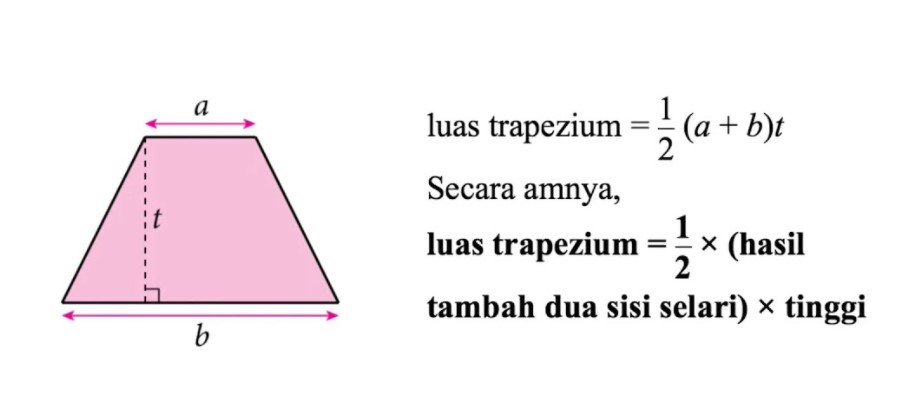
Pertama yang akan dibahas dalam artikel ini adalah tentang definisi dari trapesium itu sendiri. Jadi apa yang disebut dengan trapesium?
Adalah bangun datar dua dimensi yang dibentuk oleh 4 buah sisi, dimana dua di antaranya sejajar tapi tidak sama panjang.
Sifat-Sifat Trapesium
Berdasarkan deskripsi di atas kita telah mendapatkan gambaran tentang bentuk dari trapesium, sehingga bisa ketahui bahwa sifat-sifat dari trapesium adalah:
- Bangun datar yang memiliki 4 sisi (quadrilateral)
- 2 sisinya sejajar tapi tidak sama panjang
- Mempunyai 4 titik sudut
- Paling tidak mempunyai 1 sudut tumpul
- Terdapat 1 simetri putar
Manfaat Mempelajari Trapesium
Lalu kenapa sih harus mempalajari trapesium? Apa gunanya dalam kehidupan sehari-hari? apakah itu penting?
Tentu kita tahu segala seuatu yang ada dibumi ini pasti berguna untuk kehidupan begitu juga dengan trapesium.
Paling tidak dengan mengetahu cara menghitung trapesium kita jadi bisa menghitung luas tanah yang berbentuk trapesium.
Itu hanya contoh kecil masih ada kegunaan lain yang sangat berguna untuk bidang-bidang tertentu.
Jenis-Jenis Trapesium
Bentuk dari trapesium cukup beragam, dan tentunya dari semua ragam tersebut masih tetap mengandung unsur-unsur atau sifat dari prinsip trapesium.
Untuk mengetahui lebih jelas lagi apa saja jenis dari trapesium tersebut yuk simak penjelasan di bawah ini:
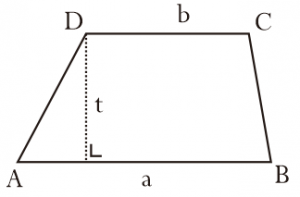
Trapesium tak beraturan
Trapsium ini juga dikenal dengan trapesium sembarang karena memang tidak memiliki kekhususan tertentu. Coba perhatikan gambar berikut ini:
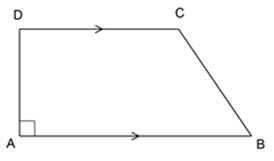
Trapesium siku-siku
Jenis yang kedua disebut dengan trapesium siku-siku.
Mengapa demikian? Karena memang trapesium ini mempunyai dua sudut siku-siku dimana keduanya sejajar dan tegak lurus dengan rusuk tinggi trapesium.
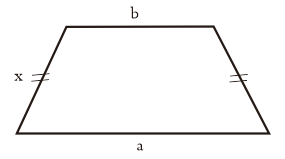
Trapesium sama kaki
Lalu selanjutnya jenis trapesium yang terakhir dinamakan dengan trapesium sama kaki ini merupakan yang mempunyai rusuk sejajar dan sama panjang, juga mempunyai 1 simetri lipat.
Rumus Trapesium
Adapun untuk menghitung sebuah trapesium kita harus mengetahui konsep atau rumus yang digunakan, dimana rumus ini akan memudahkan kita menemukan jawabannya.
Adapun rumus-rumus yang biasanya digunakan dalam menghitung trapesium adalah sebagai berikut:
Luas trapesium : L=1/2 x (a+b) x t atau L= ((a+b)x t)/2
Keliling trapesium : Kll = AB + BC + CD + DA
Tinggi : t= (2 x L)/((a+b))
Sisi a (CD) : a=(2 x L)/t-b atau CD=Kll-AB-BC-AD
Sisi b (AB): b=(2 x L)/t-a atau AB=Kll-CD-BC-AD
Contoh Soal
Supaya teman-teman bisa memahami rumus tersebut dengan mudah alangkah baiknya kalau kalian mencoba untuk menjawab contoh soal di bawah ini:
Contoh 1
Sebuah trapesium mempunyai sisi sejajar masing-masing 10 cm dan 12 cm serta memiliki tinggi 8 cm. Luas trapesium tersebut ialah …
Jawab:
L adalah ½ × jumlah rusuk sejajar × tinggi
L adalah ½ × (10 + 12) × 8 = 88 cm²
Contoh 2
Hitunglah keliling trapesium berikut ini!
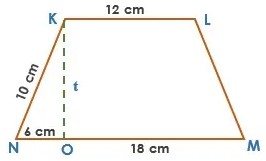
Jawab:
Karena trapesium KLMN diatas ialah trapesium sama kaki maka panjang LM = KN = 10 cm.
Sehingga kelilingnya adalah :
Keliling = KL + LM +MN + KN
Keliling = 12 + 10 + (18 + 6) + 10 = 56 cm
Demikian penjelasan kami mengenai Rumus Trapesium. Semoga bermanfaat.
Originally posted 2021-01-16 01:05:33.